SPSSで1要因ANOVA(被験者間)を行う方法と、結果の見方と書き方
サンプルデータ
SPSSで1要因ANOVA(被験者間)を行うための手順について示していきます。対象となるSPSSはバージョン27です。3つの異なる条件それぞれ被験者を20人ずつ割り当てて実験を行い、各実験後に何らかの評価(アンケートやテストなど)を取得して比較する場合、被験者間1要因ANOVAを利用できます。例えば、以下のようなデータを取得した場合を想定します:
Condition Value
1.00 101.00
1.00 103.00
1.00 101.00
1.00 103.00
1.00 98.00
1.00 105.00
1.00 97.00
1.00 93.00
1.00 92.00
1.00 102.00
1.00 104.00
1.00 97.00
1.00 94.00
1.00 104.00
1.00 103.00
1.00 100.00
1.00 103.00
1.00 99.00
1.00 95.00
1.00 99.00
2.00 53.00
2.00 52.00
2.00 52.00
2.00 50.00
2.00 46.00
2.00 50.00
2.00 43.00
2.00 57.00
2.00 51.00
2.00 36.00
2.00 52.00
2.00 51.00
2.00 58.00
2.00 49.00
2.00 51.00
2.00 61.00
2.00 56.00
2.00 50.00
2.00 40.00
2.00 36.00
3.00 13.00
3.00 11.00
3.00 26.00
3.00 19.00
3.00 16.00
3.00 30.00
3.00 18.00
3.00 21.00
3.00 17.00
3.00 13.00
3.00 19.00
3.00 14.00
3.00 24.00
3.00 18.00
3.00 26.00
3.00 19.00
3.00 17.00
3.00 16.00
3.00 27.00
3.00 26.00分析方法の選び方
SPSSから分析を行うには、メニューから分析方法を選んでいく場合と、シンタックスと呼ばれるコマンドを記入して行う場合のどちらかを選べます。メニューから対応のある検定を行う場合、「分析」→「一般線形モデル」→「1変量」を選んでください。
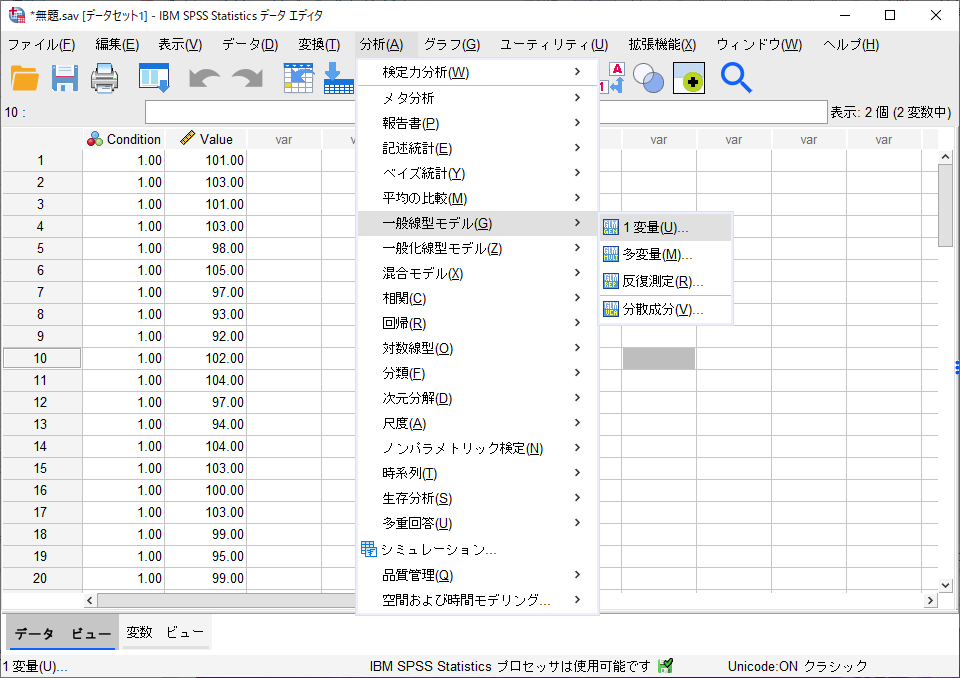
その後、「固定因子」に条件を(ここではCondition)、従属変数(ここではValue)をセットします。
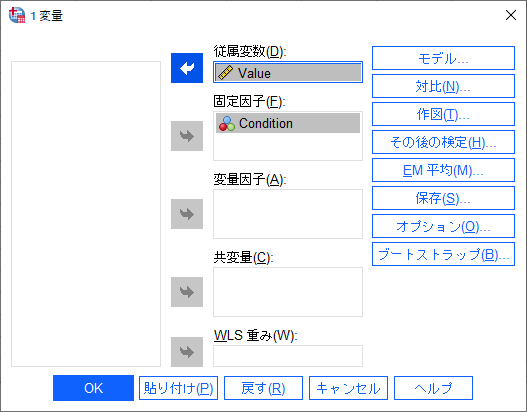
次に「その後の検定」ボタンを押して、因子のConditionを選択、矢印をクリックして右側のボックスに表示されるようにしておきます。また、下にある「Bonferroni」にチェックを入れて「続行」ボタンを押してください。
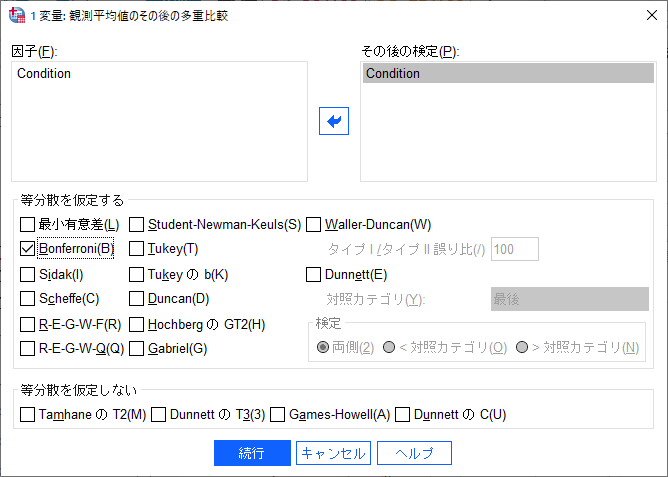
次に「EM平均」ボタンをクリックし、先ほどと同じように(OVERALL)とConditionを右側のボックスに移動します。さらに、主効果の比較にチェックを入れ、信頼区間の調整にもBonferroniをセットしておきます。
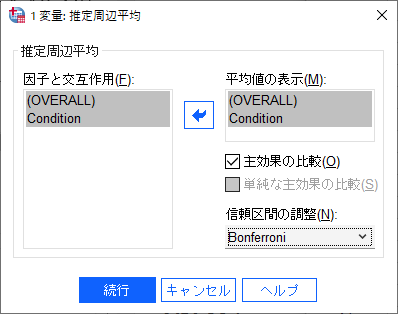
次に「オプション」ボタンをクリックし、記述統計・効果サイズ・観察検定力・等分散性にチェックを入れます。
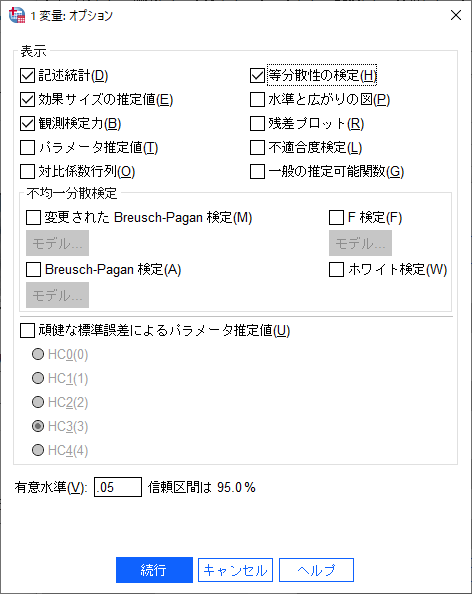
なお、下の方にある「貼り付け」ボタンをクリックすると、「1要因ANOVA(被験者間)」を実行するためのシンタックスが別ウィンドウに貼り付けられます。
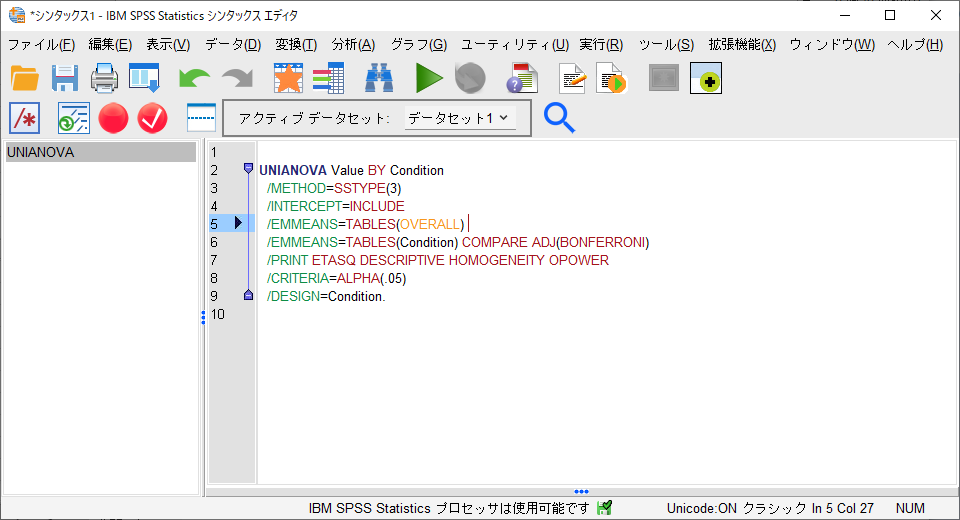
結果の見方と書き方
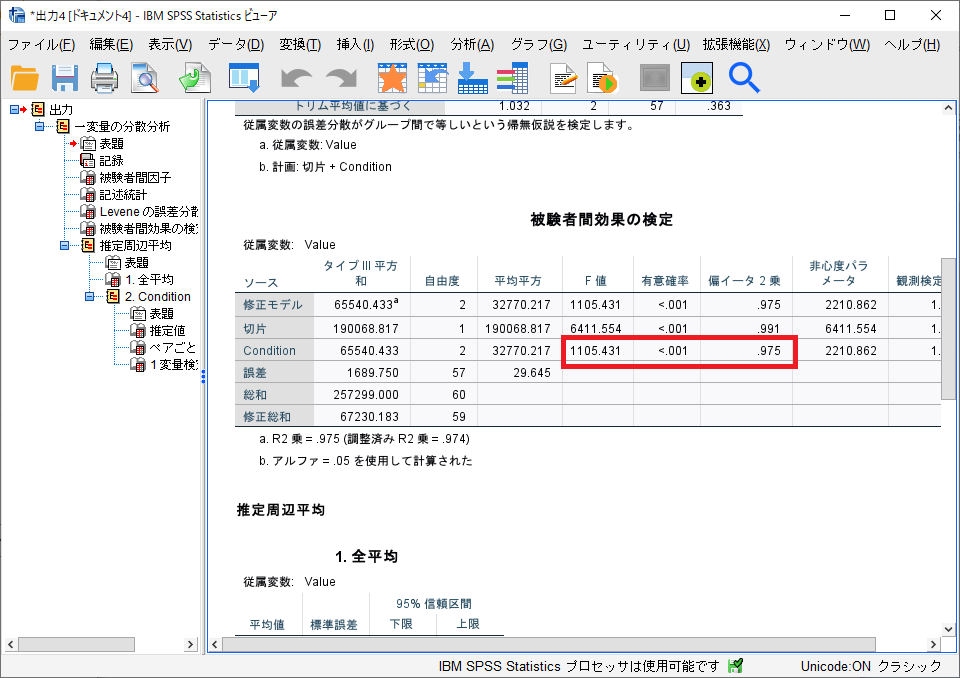
結果を見るには、「被験者間効果の検定」部分を見てください。有意確率が0.05より小さければ、いわゆる有意差があることを示しています。また、その右にある「偏イータ2乗」は、分散分析における効果サイズを意味しています。
今回は条件が3つあるので、条件内のどこに差があるかを検討する多重比較が必要となります。少し下の方にある、実験条件の分析に関する「ペアごとの比較」部分を見てください。ここに、各条件間の組み合わせにおける有意確率が示されています。ここでは、条件1が条件2/3と比べて有意差があること、条件2が条件3と比べて有意差があること、が示されています。以下に、この結果に基づいて実験結果を記載する場合の例を示します。
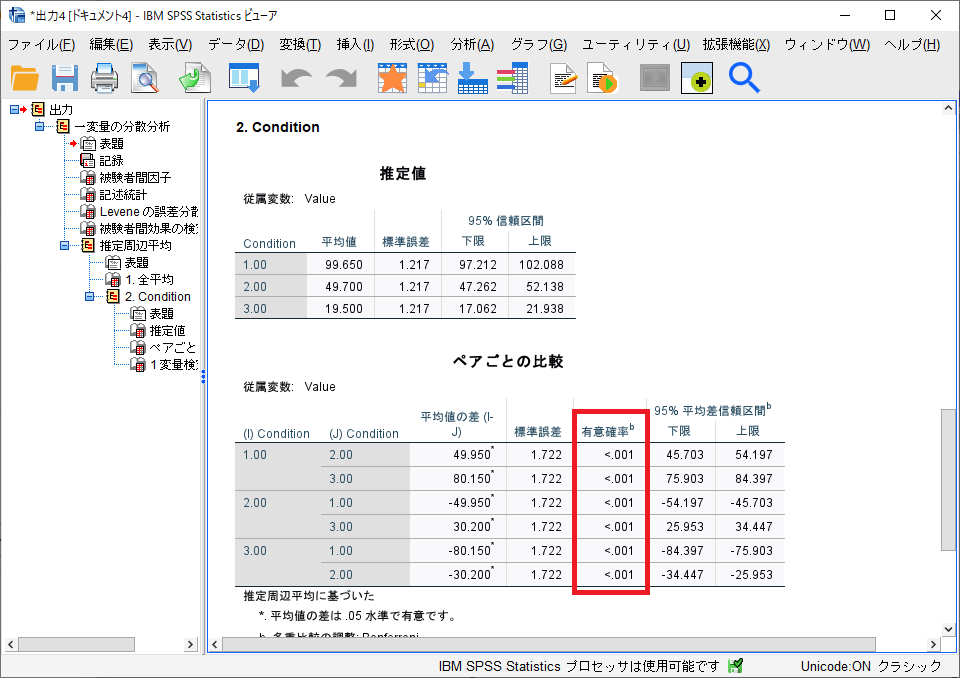
実験で取得した、各条件における刺激提示の後に得られたテスト結果に対して、被験者間1要因分散分析を行った。その結果、条件要因に有意な差が得られた(F(2,57)=1105.431, p<0.001, partial η2=0.975)。Bonferroni法による多重比較の結果、以下の組み合わせにおいて有意な差が得られた(1>2, p<0.001, 1>3, p<0.001, 2>3, p<0.001)。 すなわち、条件1において、条件2および3よりも有意に高いテスト結果が得られた。

ディスカッション
コメント一覧
まだ、コメントがありません